COSTRUZIONE - Le Meridiane di Alberto Rebora
Menu principale:
- HOME PAGE
- UNA PASSIONE NATA PER CASO
- LA RICERCA
- GNOMONICA
- GALLERIA FOTOGRAFICA
- GLOSSARIO
- LINKS
- CONTATTI
- FONTI E BIBLIOGRAFIA

COSTRUZIONE
Il nostro attuale sistema orario si basa sul giorno di ventiquattro ore di sessanta minuti ciascuna. La giornata inizia dalla mezzanotte. Gli orologi solari più comuni utilizzano questo sistema di misurazione detto anche a ore francesi.
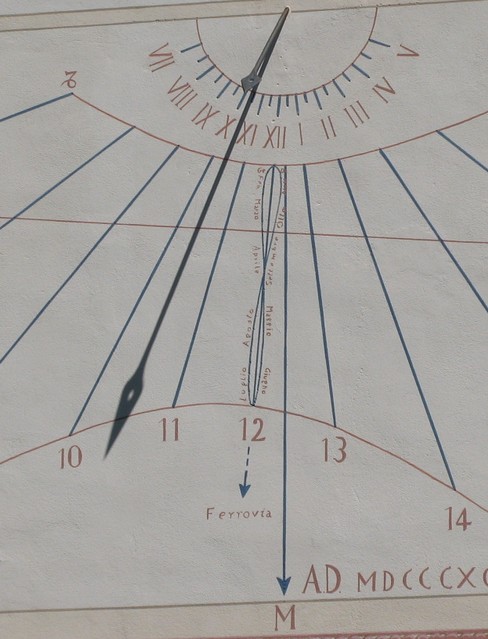
Nel film Cast Away l’attore Tom Hanks interpreta Chuck Noland un ingegnere della FedEx, corriere espresso internazionale, che dopo un ammaraggio di fortuna naufraga su di un isolotto in mezzo al mare. Di colpo si trova catapultato in quel luogo dove, perduto ogni bene materiale, è assalito dal senso di abbandono che tende a obliare anche gli affetti. Egli deve badare a se stesso in un mondo che non è più misurato dalle cose che ha perso e quindi si sente fuori del tempo. Proprio quel tempo che con la sua meticolosa organizzazione sfidava ogni giorno per consegnare le merci . Così come Robinson Crusoe organizza la sua giornata con nuove cose rimediate qua e là dal naufragio. Si crea anche un amico, Wilson di cui disegna il volto su di una palla che era a bordo dell’aereo. In attesa di essere ritrovato, ogni giorno alla stessa ora, segna la posizione di un bollo di luce di Sole fino a ottenere dopo un anno una lemniscata (la curva a forma di otto cui accennavo in precedenza).Un calendario che Chuck, si capisce, usa nei quattro anni di permanenza prima che sia ritrovato. Il raggio di luce proviene da un foro e descrive il movimento in declinazione del Sole durante l’anno scendendo in sei mesi e risalendo lungo la lemniscata in altrettanti . A Chuck bastava avere un’ora che fungesse da segnale orario e un calendario. Segnando più ore del giorno si ottiene un quadrante solare a tempo medio, quello per intenderci che mostrano i nostri orologi.
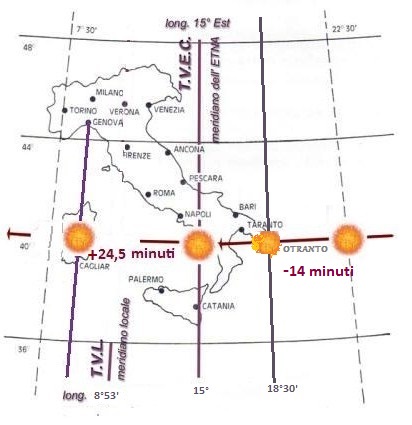
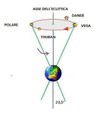
La gran parte degli orologi solari invece misura il tempo vero locale legato al moto non uniforme del Sole e le linee orarie sono rette. Ho detto locale perché ogni meridiana mostra il tempo del passaggio del Sole alla propria longitudine. A Catania e precisamente per l’Etna passa il meridiano del fuso orario dell’Europa Centrale(il nostro fuso orario). Là il Sole sorge 24’ 30’’ prima che a Genova e 14’ circa dopo che è sorto ad Otranto . L’ora vera di una meridiana costruita ad Otranto è in anticipo e quella di Genova in ritardo rispetto all’ora vera dell’Etna. Questa differenza quando è riferita ad un’orario uniformato è detta "costante locale"
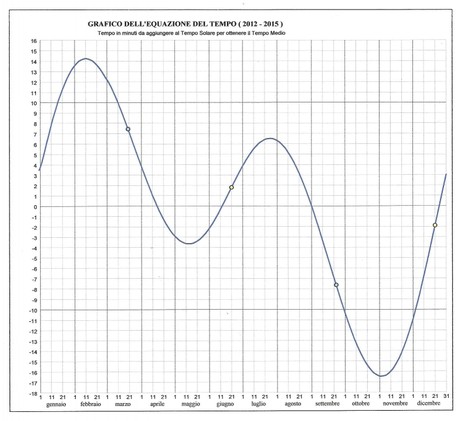
Per avere l’ora media locale bisogna aggiungere algebricamente la quantità data dall’equazione del tempo all’ora vera .
Sin da quando furono in uso, gli orologi meccanici vennero messi a punto sull’ora vera della meridiana che segnava il tempo ufficiale locale. Alcune meridiane erano costruite con una linea oraria a forma di lemniscata per mostrare il tempo medio locale. Dagli inizi dell’Ottocento il tempo medio locale, a seguito dello sviluppo degli scambi commerciali e quindi dell’espansione della rete ferroviaria, non è più sufficiente. Infatti si fa urgente la necessità di uniformare la misurazione del tempo per aree regionali, il tempo medio del capoluogo di regione diventa l’ora comune. Gli orologi solari sempre più spesso costruiti con la lemniscata per il tempo medio (di solito posta sull’ora di mezzogiorno) sono sincronizzati sull’ora regionale e dopo il 1866 sul fuso orario nazionale (fissato sul meridiano di Roma). Nel 1893 l’Italia aderisce alla Convenzione internazionale dei fusi orari ed adotta il fuso dell’ Europa centrale E1 (che passa per il cratere dell’Etna). L’ora media degli orologi meccanici ora sintonizzati sul fuso prende il sopravvento su quella fornita dalle meridiane che però per qualche decennio restano ancora un ottimo segnale orario. Poi con l’avvento della radio il loro utilizzo in pratica verrà meno.
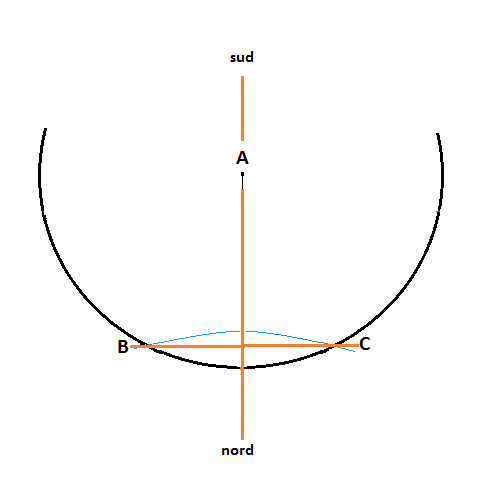
Per costruire un orologio solare è conveniente saper individuare la direzione nord-
Inoltre è necessario conoscere la latitudine del luogo dove s’installa il quadrante. La si può trovare con lo stilo appena usato, ma bisogna attendere l’equinozio oppure i solstizi e misurare la lunghezza dell’ombra dello stilo al mezzogiorno vero. Ancora non molto tempo si usava una cartina geografica (possibilmente militare 1:25.000,ma da 50.000 va bene ugualmente) che fornisce anche la longitudine. Volendo giocare col sestante è sufficiente misurare l’altezza della Stella Polare per avere la latitudine, oppure l’altezza del Sole quando passa al meridiano locale che ci dà la colatitudine . Oggi più semplicemente con Google o con un telefonino dotato di GPS possiamo conoscere latitudine e longitudine in modo immediato e sufficientemente preciso. Poi in base al tipo di quadrante che vogliamo realizzare, dobbiamo fare altre misurazioni per verificare l’inclinazione del quadro rispetto allo zenit e calcolare l’orientamento del quadrante rispetto a sud. Dovremo infine arrivare a conoscere quello che chiamo enfaticamente il DNA del nostro orologio: il triangolo stilare e la sua distanza angolare dalla linea di massima pendenza. In realtà non si tratta di una vera e propria matrice che ne contraddistingue l’unicità. Infatti si possono realizzare orologi equivalenti per piani e luoghi differenti, ma aventi la stessa altezza stilare. Quindi in pratica ogni orologio costruito in un luogo è unico perché non funziona in altro luogo che quello salvo, come ho detto, cambiare il posizionamento del quadrante. Quindi per costruire o restaurare un quadrante solare dobbiamo fare riferimento a quella matrice da trovare con riga e compasso o con il calcolo.
Orologio verticale declinante
a) costruzione mediante disegno geometrico
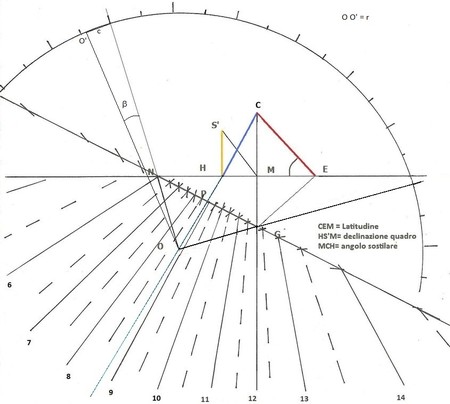
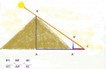
Prendiamo un falso stilo cioè un’asta mobile che chiamiamo HS fissata ortogonalmente a una base e lo collochiamo a piacere su di un muro verticale declinante(che non guarda esattamente a sud) * , dove più frequentemente capita di costruire una meridiana. Tracciamo una linea orizzontale (orizzonte) che facciamo passare per la base H dello stilo. (fig. 1)
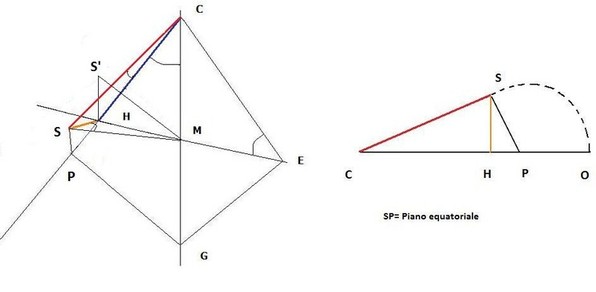
Essa rappresenta la linea del sorgere e del tramonto del Sole. Infatti il Sole durante la sua escursione diurna dall’alba al tramonto si troverà sempre al di sopra di essa e lo gnomone farà ombra sul quadrante sottostante dove sono disegnate le linee orarie. Premesso che conosciamo la nostra longitudine e abbiamo una tabella dell’equazione del tempo, troviamo l’ora media corrispondente al mezzogiorno vero e in quell’istante segniamo l’ombra della punta dello stilo. In alternativa il mezzogiorno vero si trova con un falso stilo attendendo il momento in cui la sua punta indica la linea nord sud che precedentemente avevamo trovato. Tracciamo una linea verticale per quel punto ** e abbiamo la linea meridiana che intersecherà l’orizzonte nel punto M. Se la parete non fosse declinante, esso cadrebbe a piombo sotto la radice dello stilo, mentre si troverà a sinistra di H se il quadrante è declinante est e a destra con declinazione ovest. Ribaltiamo lo stilo sul piano verticale e otteniamo il segmento HS’, tracciamo la retta congiungente la punta S’ dello stilo e il punto M. L’angolo HS’M è la declinazione d della parete che posso anche calcolare essendo d = arcotang (HM: HS’). (fig.1 e 2a). Punto il compasso in M e ribalto MS’ in E sulla linea orizzontale. Di qui con apertura pari all’angolo della latitudine trovo lo stilo polare che interseca la linea meridiana in C centro dell’orologio solare. Da E traccio la perpendicolare allo stilo fino a incontrare la linea meridiana in G che è un punto della traccia del piano dell’equatore celeste sul quadrante (linea equinoziale). Congiungo C a H e ottengo la linea sustilare che è la proiezione dello stilo polare sul quadrante e la prolungo a piacere; da G traccio la normale a questo segmento che lo incontra in P e prolungo fino a intersecare la linea dell’orizzonte in N. GN è la linea equinoziale. L’angolo GEM è uguale alla colatitudine. Se ribaltiamo il triangolo CEG intorno alla linea meridiana CG fino a toccare la punta dello gnomone in S sarà SG = EG il segmento di retta che unisce lo gnomone con G. PSG, è il piano equatoriale(fig 2b). Se lo ribaltiamo sul piano dell’orologio solare, possiamo tracciare le linee orarie. A tale scopo basterà staccare sulla sustilare un segmento PO tale per cui GO = GE. Trovato O, lo congiungo con N, dove l’equinoziale incontra la linea dell’orizzonte. Il triangolo NOG è retto. Agli equinozi i punti G e N sono toccati rispettivamente dall’ombra dello gnomone a mezzodì e al levare del Sole se la parete e orientata a levante oppure al tramonto se la declinazione è ovest. Con centro in O e raggio a piacere traccio un arco di cerchio che comprenda il prolungamento dei lati di suddetto triangolo OG e ON e lo divido in più parti di 7,5° per avere anche le mezze ore. Lo faremo a partire dal punto G o N in cui possiamo individuare le ore 6 che corrispondono ,in base alla declinazione del quadrante, all’alba o al tramonto. Tracciamo i raggi delle relative divisioni da O fino a incontrare la linea equinoziale. Per i punti trovati passano le linee orarie che convergono tutte in C. Se il quadrante solare è di grandi dimensioni per costruire gli angoli è consigliabile usare le formule trigonometriche anziché il goniometro.
CM = ME tang φ; MG = ME tang (90-
essendo MS = HS : cos d . Otteniamo così la rete oraria di un orologio solare che segna l’ora locale.
Poi installeremo lo stilo ortogonale HS della lunghezza del falso stilo che avevamo usato per costruire la rete. Quello poc’anzi descritto è uno dei tanti metodi per costruire un quadrante solare a ora vera con le proiezioni geometriche. Per ottenere l’ora vera del fuso dell’Etna bisogna adeguare la nostra longitudine ruotando l’arco di cerchio definito dall’angolo NOG in senso orario se ci troviamo a levante rispetto ad esso e viceversa se siamo a ponente.
Ad esempio se ci troviamo in un punto di Genova che è 6° 6’ a ponente del meridiano dell’Etna essendo la sua longitudine 8° 54’ E dovremo ruotare l’arco anzi detto in senso antiorario di 6° 6’ "anticipando" le linee orarie di 24’ 24". Se chiamiamo r il raggio dell’arco e β l’angolo che rappresenta la differenza di longitudine troveremo la corda c che definisce la quantità di spostamento delle linee orarie essendo c = r tang b
* Se la direzione dello stilo ortogonale è nord/sud ,e quindi coincide con quella dello stilo polare, si dice che il quadrante è meridionale.
** Quando il quadrante declinante è inclinato rispetto allo zenit la linea meridiana non coincide con quella di massima pendenza, mentre la linea meridiana è a piombo nel quadrante inclinato meridionale.
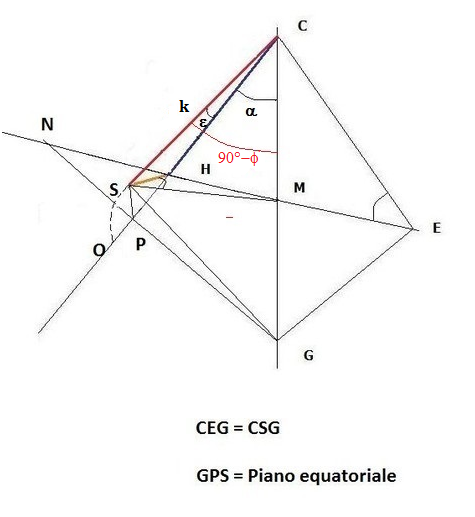
Per installare lo stilo polare di cui conosciamo la lunghezza , basta fissarlo al punto C in modo che l’altra estremità coincida con S che è la punta del falso stilo. Poiché questa operazione non è facile , in pratica è consigliabile costruire una dima triangolare delle dimensioni del triangolo stilare CHS (il nostro DNA) che volendo funge benissimo da gnomone (fig. 2 a,b). Si fisserà al muro sul lato CH che coincide con la sustilare. La sua distanza angolare a dalla linea verticale (che in questo caso coincide con la linea meridiana) , detta distanza sustilare , qui è MCH = arcotang ( HM:MC) , dove HM è misurabile sul muro . CH è calcolabile con Pitagora essendo l’ipotenusa del triangolo retto CHM di cui conosciamo i cateti HM e CM. La dima opportunamente adattata servirà da sostegno per l’installazione di uno stilo a bacchetta. E’ utile considerare anche le seguenti relazioni.
CM =κ senφ; MS = κcosφ; MH = MScos(90-
tang α = MH/MC = kcosφsend/ksenφ = sendcotφ
HCS = arcotang (HS/CH) fig. 2) è l’altezza dello stilo (detta altezza sustilare) che varia in funzione della declinazione del muro e della latitudine. Infatti
ε = arcosen (HS/CS) = kcosφcosd/k = cosφcosd
Il punto geometrico S dove l’ortostilo HS coincide con lo stilo polare CS è detto gnomonico. Materialmente è il cuore funzionante dello gnomone di solito fatto a forma di nodo, oppure un taglio, un foro, una sferetta, la punta dello stilo che vanno usati a guisa di mirino da chi legge l’orologio solare. L’ombra di tale punto proiettata sulla rete delle linee orarie e diurne descrive la posizione del Sole in ogni momento della giornata e dell’anno. Negli orologi più semplici di solito le linee diurne non sono presenti.
L’orologio solare si può costruire geometricamente con squadra e compasso direttamente sul quadrante oppure facendo il disegno su un foglio a spolvero poi riportandolo sul quadrante. Aiutandoci con il calcolo matematico possiamo evitare gli errori di misurazione e riporto degli angoli quando vogliamo costruire un orologio di grandi dimensioni e quindi necessitiamo di maggiore precisione.
Se vogliamo fare a meno della costruzione geometrica , possiamo calcolare la lunghezza dello stilo polare e i dati per sistemarlo opportunamente. A tale scopo è sufficiente stabilire la lunghezza dello stilo ortogonale HS e conoscere latitudine e declinazione gnomonica. Misurata la distanza HM della base dell’ortostilo dalla linea meridiana con il metodo spiegato precedentemente, abbiamo visto come trovare la declinazione gnomonica (vedi anche Gnomonica-
MS = HM/send CS = MS/sen(90-
Trovo la sustilare CH e CM con il teorema di Pitagora e quindi non è necessario calcolare la distanza sustilare α.
Una volta fissato lo stilo polare alla parete possiamo realizzare la nostra meridiana anche con un metodo artigianale che fa uso dell’orologio equatoriale. Si tratta di un orologio con il quadrante inclinato parallelamente all’equatore celeste che per questa particolarità ed il relativo funzionamento è considerato il padre degli orologi solari ad angolo orario. Per questo apri la finestra OROLOGIO EQUATORIALE .
b) costruzione mediante il calcolo
Se non consideriamo il calcolo vettoriale, che qualche matematico appassionato di gnomonica ha applicato negli anni recenti soprattutto per il calcolo di orologi complessi come i bifilari e i trifilari, normalmente si fa uso della trigonometria sferica che descrive astronomicamente l’orologio solare inquadrandone lo studio all’interno della sfera celeste.
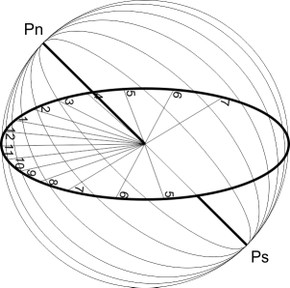
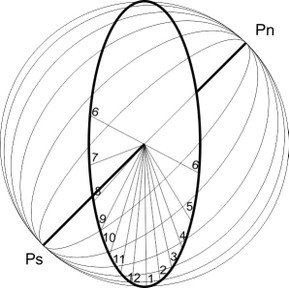
Le due sfere seguenti ci mostrano rispettivamente un quadrante orizzontale e uno verticale meridionale. Entrambi sono orientati esattamente a sud.
Ovviamente possiamo dare al quadrante altre posizioni:
a) variare sul piano orizzontale il suo azimut rispetto alla linea meridiana (meridiana declinante)
b) modificare la sua inclinazione rispetto al piano orizzontale che si considera d’ inclinazione 90° rispetto allo zenit e 0° per il quadrante verticale.
c) variare declinazione e inclinazione contemporaneamente.
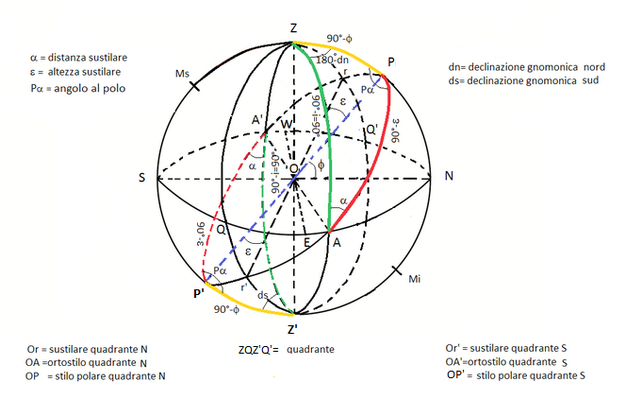
Quest’ultimo caso è quello che si riferisce ad un quadro comunque orientato che è il più complesso dei tre. La figura 4 ci mostra il quadro QZQ’Z’ il cui orientamento è dato dal punto A del segmento OA perpendicolare al piano del quadro. Poiché A si trova sul piano dell’orizzonte l’inclinazione del quadro è 0° ed il suo orientamento a nord est è direttamente riscontrabile nel disegno. Specularmente il punto A’ dello stilo OA’ indica la declinazione gnomonica a sud ovest per la faccia sud del nostro quadrante. Ci troviamo nel caso a) di un quadrante declinante verticale che per un costruttore di orologi solari, si diceva, è il più frequente.
Il triangolo sferico ZAPn ci permettere di ricavare e e α applicando la formula del coseno da cui derivano quelle precedentemente viste che si usano per calcolare angolo orario, azimut e altezza dell’astro. Così partendo dalla formula cosc = cosacosb + senasenbcosγ abbiamo:
senε = senφseni -
che nel triangolo rettilatero ( con i = 0° e quindi il lato ZA = 90° ) diventa
sen ε = -
senα = send cosφ /cosε Trovati i due angoli suddetti non siamo ancora in grado d’installare lo stilo polare noto , infatti bisogna almeno calcolare la lunghezza della sustilare che è Or = kcosε . Poi dovremo trovare le linee orarie che alcuni autori calcolano partendo dall’ora della linea sustilare (la linea di simmetria della rete oraria) mentre altri si basano sulla linea meridiana. L’ora sustilare si ricava tramite il suo angolo al polo
sen Pa = sen d/cos e
Successivamente si trovano le altre ore calcolando la loro distanza angolare dalla sustilare misurata sul quadrante.
Per gli orologi verticali declinanti trovo sia più semplice calcolare le linee orarie facendo riferimento al meridiano locale.
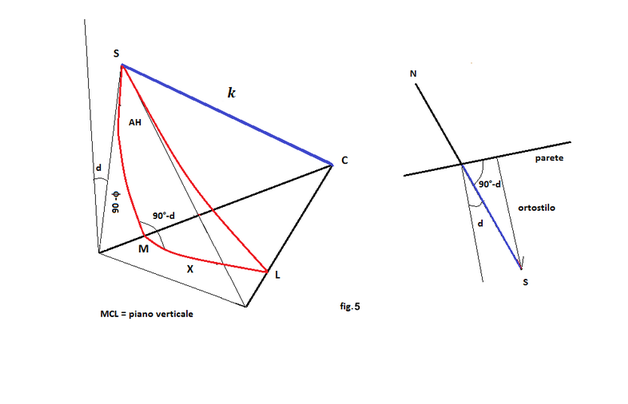
Preso il triedro formato da tre linee rette identificate dai segmenti CS = lo stilo polare , C L una linea oraria e C M la linea meridiana e preso CS come il raggio della sfera di centro C consideriamo il triangolo sferico SML risultante dall’intersezione della sfera con le tre rette fig. 5 .
La formula cotgbsena = cosaseng + sengcotgb applicata al nostro triangolo diventa
![]()
![]()
Negli ultimi anni sono stati pubblicati diversi volumi che trattano l’argomento e lo risolvono con la trigonometria piana, sferica e più ampiamente con l’analisi matematica fino al calcolo vettoriale 1). Comunque sia progettare un orologio solare con il calcolo manuale, seppure aiutati da una calcolatrice portatile, richiede non poco tempo. Oggi programmi per il calcolo di orologi solari di vario tipo sono reperibili sul web e con essi è agevole calcolare orologi solari e modificarne le caratteristiche in fase di progettazione.
1) per quest’ultimo vedi ad esempio
Denis Savoie, La Gnomonique 2007 che tratta anche del calcolo vettoriale e recentemente.
Francesco Caviglia, Strumenti per la gnomonica vettoriale in Atti del XIX Seminario Nazionale di Gnomonica,Cefalù,4/2014
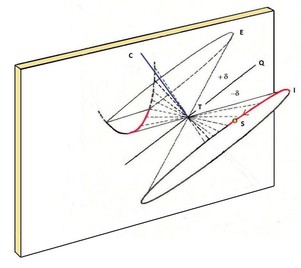
Linee diurne
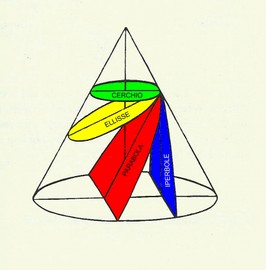
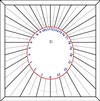
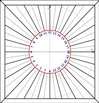
Abbiamo visto che la declinazione del Sole varia da – 23° 27’ A + 23°27’ e quando passa per l’equatore la sua declinazione è 0°. Consideriamo l’asse Sole Terra quando siamo all’equinozio, il Sole descrive un piano su cui giace la circonferenza massima dell’equatore, lo strumento equatoriale che abbiamo preparato per disegnare le ore della meridiana lo rappresenta materialmente bene. Man mano che il Sole al variare della sua declinazione si allontana dall’equatore Q, l’asse TS genera dei coni che sono compresi tra i due solstizi. Possiamo vedere come funziona nel disegno se facciamo coincidere il punto T col punto gnomonico di uno stilo polare da cui,come si vede nel disegno parte il raggio del piano dell’equatore Q ad esso perpendicolare. Ancora da T partiranno dei raggi in direzione del Sole in E ed I che formeranno ciascuno un angolo di massima declinazione di 23° 27’. I coni generati dall’asse TS intersecando il quadro dell’orologio solare assumeranno le diverse forme di sezioni coniche che dipendono dall’inclinazione e del quadro rispetto all’equatore in relazione alla declinazione del Sole d . Se ad es. prendiamo un quadrante orizzontale, risulta che, rispetto al piano dell’equatore, e = 90° e al polo e = 0°, quindi per questo quadrante e = colatitudine. In generale per qualunque inclinazione del quadrante avremo le seguenti figure:

Trigono
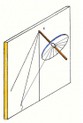
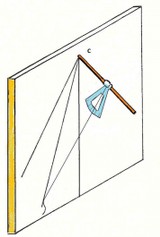
Per disegnare le linee diurne ci si può attrezzare con un trigono (o sciaterre alla francese) fig.1a.
Su questo strumento che assomiglia a una scure è segnata la graduazione degli angoli di declinazione solare che vogliamo disegnare sul nostro orologio. Di solito si tracciano almeno le linee dei solstizi e quella equinoziale. Il punto di riferimento come per le linee orarie è il punto gnomonico (vedi triangolo stilare). Lo strumento ruota sul piano equatoriale intorno allo stilo polare e deve essere allineato ai piani orari secondo i relativi angoli orari. Sempre con l’aiuto di un filo si prolunga ciascuna linea relativa all’angolo di declinazione ( materializzazione della linea generatrice della conica che all’inizio abbiamo chiamato TS) fino ad intercettare la linea oraria. Così facendo per tutte le linee orarie troveremo una serie di punti che congiunti ci permetteranno di disegnare la conica che cercavamo.
Lunghezze d’ombra
Il trigono essendo usato direttamente sul quadrante richiede una buona manualità senza la quale non si ottengono risultati soddisfacenti. Quindi col tempo l’uso di questo attrezzo si è perso. Oggi si usano metodi grafici e di calcolo che permettono di costruire orologi solari anche di notevole precisione. Peraltro è possibile calcolare le linee diurne tramite le equazioni relative ad ogni tipo di curva (iperbole, parabola ecc.) che poi sono inserite nei vari software studiati per la costruzione delle meridiane.
Un programma specifico per progettare orologi solari sebbene utilissimo non ci spiega il funzionamento degli stessi. Così se preferiamo operare cercando di capire tale funzionamento possiamo farlo sia con la geometria che calcolando le lunghezze d’ombra ad ogni ora o frazione. A questo scopo basta tradurre in geometria quanto si fa in pratica come si è visto prima usando il trigono(fig. 1b)
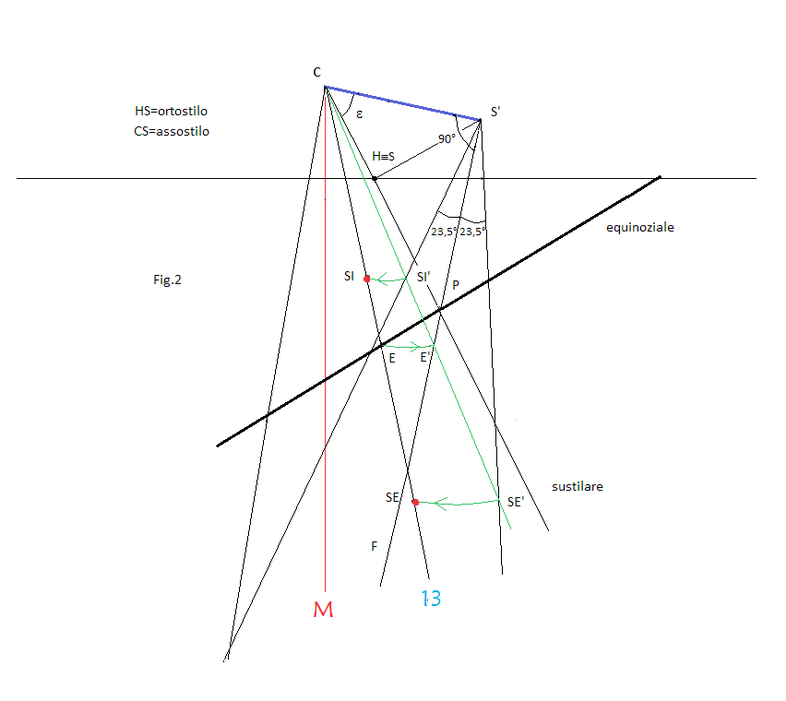
Nella costruzione geometrica ( fig. 2) l’allineamento della lama sul piano orario si risolve col ribaltamento del triangolo stilare CHS intorno alla sustilare sul piano dell’orologio. Lo stilo ortogonale HS con origine in H formerà con lo stilo polare il triangolo ribaltato CHS’ dove S’ è il punto gnomonico aereo S ribaltato.
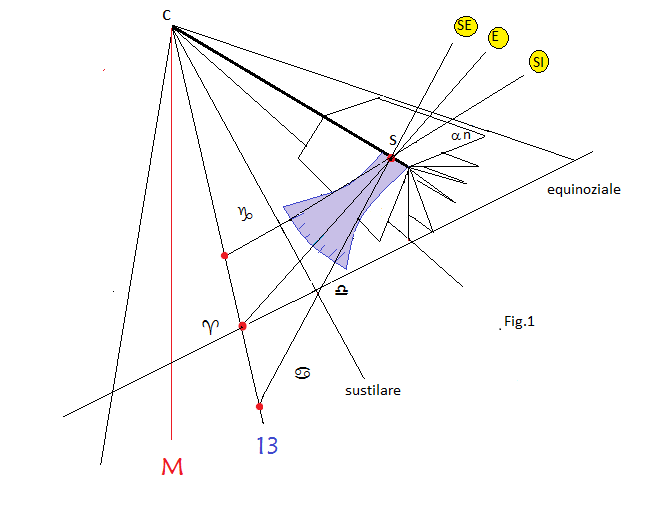
Dal punto gnomonico S’ si tracciano le linee delle declinazioni solari che corrispondono alle stesse tracciate sulla lama graduata del trigono. Il raggio S’F (perpendicolare allo stilo in S’ ) di declinazione 0° intercetta il punto P in cui la sustilare interseca la linea equinoziale che è tracciata sull’orologio. PS’ è la sezione laterale del piano equatoriale, da S’ si costruiscono due angoli uguali di 23,5° ciascuno simmetrici rispetto a S’F che rappresentano le declinazioni massime dei solstizi all’interno dei quali si possono tracciare altre declinazioni. Conviene tenere fermo il trigono e spostare le linee orarie. Scelta una linea individuiamo il punto E d’intersezione con l’equatoriale e con centro in C e apertura CE portiamo il punto E in E’ che intercettiamo sul raggio S’F. La semiretta che da C passa per E’ è la linea oraria ribaltata che è intersecata dai raggi di declinazione solstiziali SE’ e SI’.E’ sufficiente riportare tali punti a ritroso sulla linea oraria per ottenere i punti cercati SE e SI. Fatta la stessa operazione per le altre linee orarie si ottengono i punti su cui avviare le linee diurne cercate.
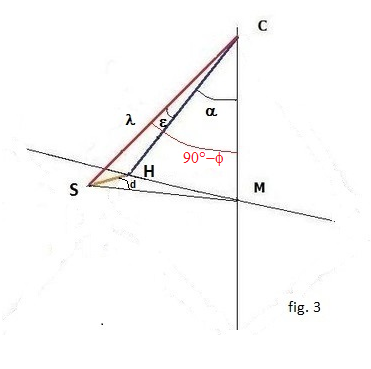
Calcolo delle lunghezze d’ombra.
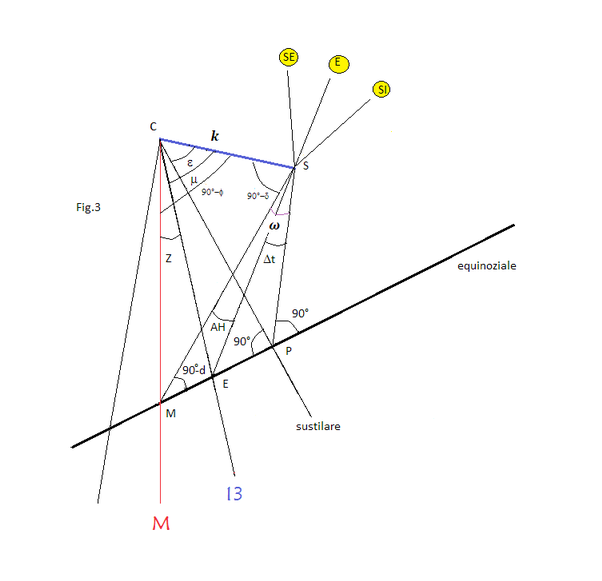
Nota la lunghezza dello stilo polare CS (fig. 3 ),scegliamo la linea oraria su cui calcolare la lunghezza d’ombra CE dove C è il centro dell’orologio ed E il punto dove la linea oraria incontra la linea equinoziale essendo in quel giorno la declinazione solare di 0° 1.).A tale scopo dobbiamo calcolare l’angolo aereo m compreso tra la linea oraria e lo stilo. Abbiamo visto che i piani orari ruotano intorno allo stilo la cui proiezione sul quadro, detta linea sustilare, è l’asse di simmetria delle linee orarie che è perpendicolare alla linea equinoziale.
Come si può notare alla fig. 1 la variazione della declinazione del Sole avviene sullo stesso piano orario e quindi non influenza l’angolo m
senε = cosφcosd
Dove e è l’altezza angolare dell’assostilo, j latitudine, d declinazione del quadrante
SP = CStangε ; SE = SP/cos∆t = ktangε/cos∆t ; tangμ = SE/k=tangε/cos∆t
Dt = differenza angolare tra l’ora sustilare e l’ora scelta.
L’angolo orario ω dell’ora sustilare si ha con tangω = tangd/tangφ
L’angolo orario AH dell’ora scelta si misura in ragione di 15° ogni ora a partire da mezzogiorno.
In alternativa per trovare l’angolo m si può usare la trigonometria sferica prendendo a riferimento la linea meridiana invece della sustilare, così nel diedro CSME abbiamo:
cosμ = senφcosz + cosφsenzcos(90±d)
tangz = cosφ/(senφsend+cosdcotgAH)
Z angolo tra la linea oraria e la linea meridiana tracciate sul quadro
d declinazione solare
Trovato m possiamo calcolare la lunghezza d’ombra CE, per il teorema dei seni:
CE/senESC = CS/cosSEC; CE = kcosδ/cos(m -
1)Sappiamo che la declinazione del Sole varia continuamente anche durante la giornata. Nei limiti di gran parte delle applicazioni gnomoniche la declinazione giornaliera può essere considerata costante.
Il mio viaggio nel tempo era iniziato a seguito di una passione nata per caso che tutt’ora è viva, ma l’occasione che la generò non andò a buon fine nonostante mi fossi speso non poco per la sua riuscita. Infatti avevo dovuto acquisire le conoscenze essenziali per realizzare un orologio solare, in effetti il mio amico si convinse che era buona cosa restaurare la meridiana e cercò di persuadere gli altri condomini. Purtroppo non riuscì nel suo intento e quell’orologio è ancora là ad Ovada così come si vede qua sotto.