QUADRANTI EQUIVALENTI - Le Meridiane di Alberto Rebora

QUADRANTI EQUIVALENTI

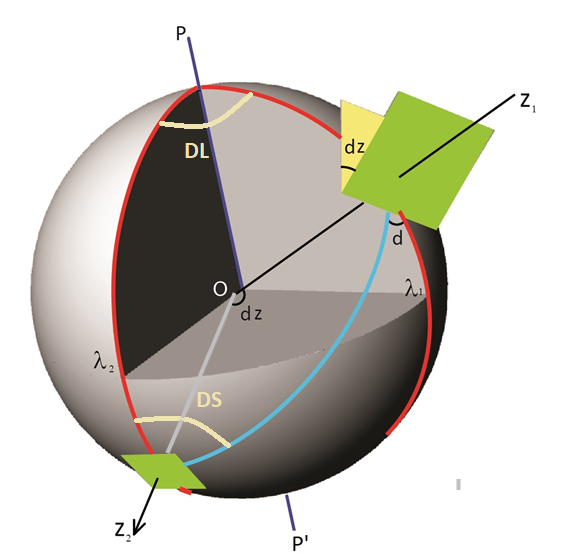
Un quadrante solare comunque orientato e costruito per una certa latitudine funziona come quadrante orizzontale a un’altra latitudine. E’ possibile trovare la nuova latitudine, che chiamiamo "equivalente", se immaginiamo di traslare il quadrante secondo la direzione della linea di massima pendenza percorrendo un cerchio massimo terrestre. Trovata la nuova latitudine sarà facile costruire il quadrante orizzontale corrispondente.  Nel caso in cui la declinazione gnomonica fosse nulla la traslazione avverrebbe secondo il meridiano locale che comprende zenit, nadir e i poli. In  un quadrante verticale declinante la traslazione è fatta lungo la linea meridiana che coincide con quella di massima pendenza. Con questo metodo si semplifica non di poco la costruzione dell’orologio solare soprattutto quando il suo quadrante si presenti declinante ed inclinato. Il piano dell’orologio durante lo spostamento deve rimanere parallelo a se stesso fino a quando non si trovi perpendicolare allo zenit della località di latitudine equivalente.  Nell’ immagine seguente è rappresentata la sfera terrestre sulla quale viene traslato un piano inclinato e declinante da  una località con zenit Z1 e latitudine j1 ad un’altra in Z2 e  j2.

Fig 1

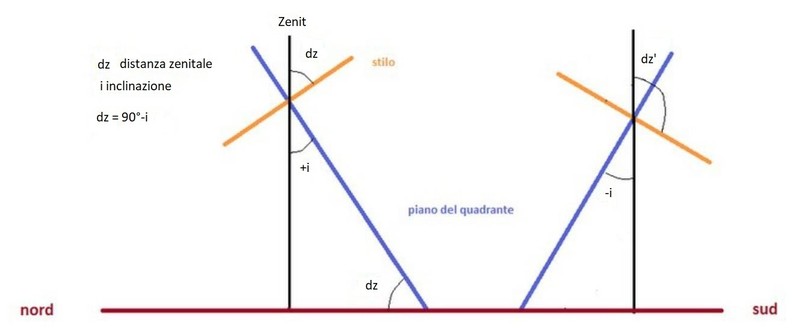
La linea azzurra (detta di massima pendenza) rappresenta il cerchio massimo di traslazione da   Z1, dove vogliamo costruire l’orologio, a  Z2 con un’ampiezza angolare dz (vedi fig. 2) che corrisponde alla distanza zenitale del quadrante di partenza

Fig.2

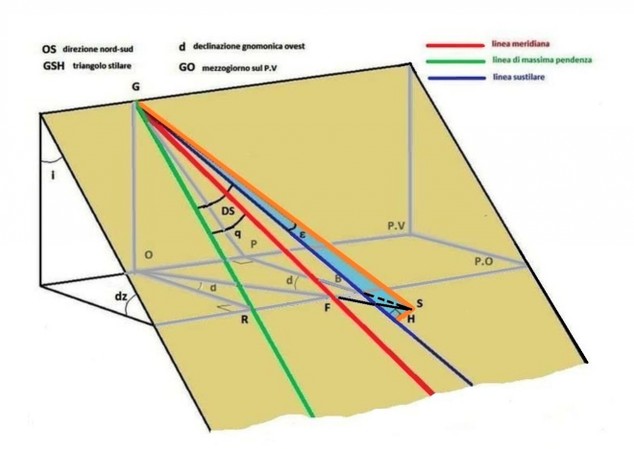
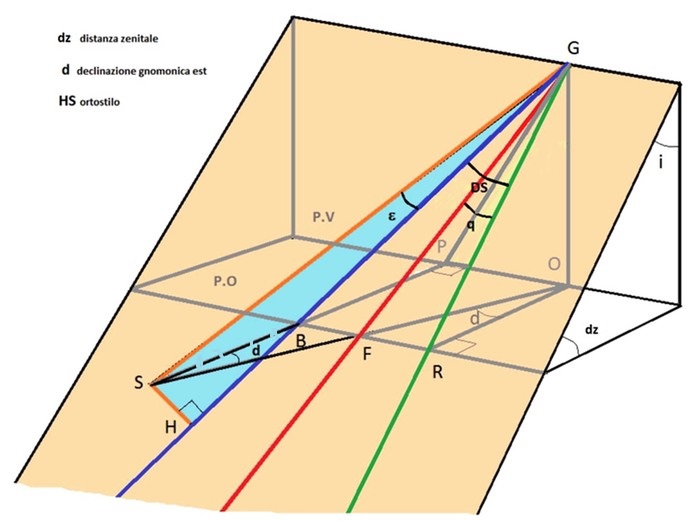
La latitudine equivalente trovata sarà l’altezza stilare dell’orologio orizzontale. La meridiana che voglio costruire avrà la stessa altezza stilare di quella equivalente, ma la sua linea sustilare non coinciderà (come in quella orizzontale) con il mezzogiorno né con la linea di massima pendenza. Pertanto in fase di realizzazione una volta tracciata la linea di massima pendenza (a piombo da un punto scelto come centro dell’orologio) riporterò la linea sustilare della meridiana orizzontale equivalente ruotata in modo che formi con essa l’angolo DS (distanza sustilare). In tal modo lo stilo sarà allineato all’asse terrestre (vedi Fig.4a e 4 b per le posizioni della sustilare rispetto alla linea a piombo e a quella meridiana in base alla declinazione gnomonica).Poiché per fare la traslazione del piano ci si è spostati di longitudine, Il tempo letto sulla meridiana equivalente a longitudine l2,sarà diverso da quello alla longitudine l1 del luogo dove vogliamo costruire il nostro quadrante. In pratica quando il Sole è al meridiano passante per Z1, l’ombra dello stilo forma con la sustilare un angolo che esprime la differenza di longitudine. Quindi dobbiamo correggere l’ora letta con una costante temporale tenendo conto del verso di traslazione se est oppure ovest.
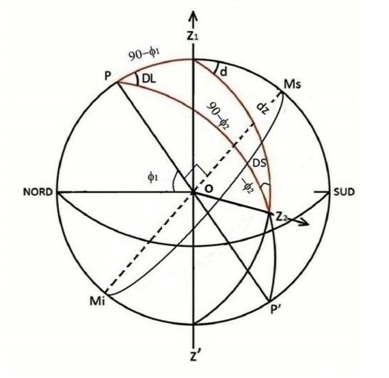
La figura 3  ci mostra il meridiano locale con zenit  Z 1  e  longitudine l1  che  immaginiamo proiettati dalla Terra sulla sfera celeste geocentrica.

Fig.3

Dal centro O della sfera si stacca la verticale al punto Z2 che è il nuovo zenit e OZ2 lo stilo ortogonale della meridiana orizzontale equivalente. Sappiamo che dz è la distanza zenitale di Z2, j2 è la latitudine equivalente da trovare, d la declinazione gnomonica, DL è l’angolo orario del punto Z2 contato dal mezzogiorno locale che corrisponde in tempo all’ora segnata dalla sustilare. DS è l’angolo tra la linea di massima pendenza del quadro e la linea sustilare detto distanza sustilare. Nel triangolo sferico PZ1Z2 ricaviamo la latitudine equivalente con la seguente formula:

senφ2 = senφ1cosdz - cosφ1sendzcosd

Nello stesso triangolo con le solite formule di trigonometria sferica si trovano DS e DL.

tang DS = send/(sendztangφ1+cosdzcosd)         tan DL = send/(cosφ1cotgdz+senφ1cosd)

Le seguenti formule possono essere usate se si conosce la latitudine equivalente:

senDS = sendcosφ1/cosφ2                                                     senDL = sendsendz/cosφ2

Infine, calcoliamo l2

cosλ2 = (sendsendzsenλ1+cosdsendzcosλ1senφ1+cosdzcosλ1cosφ1)/cosφ2  

oppure  si può ottenere per differenza tra DL e l1.


Per esempio, dati j1=44,46° l1=9,19°E  dz=30°  d=96°w;   otteniamo j2=40,84° DS= 67,22  DL= 41,09°  l2=31,90°

La differenza temporale di due ore e 44,36’ (41,09°x4’) espressa da DL è l’ora segnata dalla sustilare dell’orologio solare in costruzione che sulla meridiana orizzontale corrisponde alle 12.Così correggiamo le ore indicate dalla meridiana orizzontale con questa costante temporale e le riportiamo sulla nuova. Nel caso in esempio la nuova meridiana inclinata/declinante sarà anticipata rispetto a quella orizzontale segnando mezzogiorno quando su quest’ultima saranno le nove e 16 circa.
Per utilità e verifica si può tenere conto della relazione che fornisce l’angolo q tra la linea meridiana e quella di massima pendenza.

tangq = tangdcosdz

Vedi figg.4a, 4b.


Se non avessimo preparato lo spolvero delle ore corrette con la costante temporale , con  l’orologio equatoriale , possiamo   tracciare  le linee orarie col filo dopo aver allineato  la sua linea di mezzogiorno con la meridiana appena tracciata.  
Costruire geometricamente un orologio verticale declinante non presenta particolari difficoltà, quindi l’uso del metodo degli orologi equivalenti per questo tipo di quadrante mi sembra una complicazione, un po’ " come grattarsi l’orecchio destro con la mano sinistra". La tecnica  dei quadranti equivalenti a mio avviso è una soluzione creativa e divertente per la costruzione di orologi complessi come il quadrante inclinato e declinante che può essere impiegata in alternativa ai soliti procedimenti che già utilizziamo.

Fig 4a

Fig. 4b