IL SOLE L'OMBRA E IL TEMPO - Le Meridiane di Alberto Rebora
Menu principale:
- HOME PAGE
- UNA PASSIONE NATA PER CASO
- LA RICERCA
- GNOMONICA
- GALLERIA FOTOGRAFICA
- GLOSSARIO
- LINKS
- CONTATTI
- FONTI E BIBLIOGRAFIA

Il SOLE ,L’ OMBRA E IL TEMPO
Il movimento del nostro orologio da polso è meccanico o al quarzo, quello della meridiana è il Sole che con le sue ombre scandisce lo scorrere delle ore sul quadrante. Lo studio delle ombre solari (Scioterica) è stato alla base delle prime osservazioni scientifiche e fu applicato in astronomia fin dai suoi inizi.
Gli antichi Babilonesi nel Primo Millennio a.c. diedero la spiegazione dell’eclissi lunare osservando l’ombra della Terra proiettata sulla Luna. A loro si deve l’adozione del sistema sessagesimale in astronomia matematica.
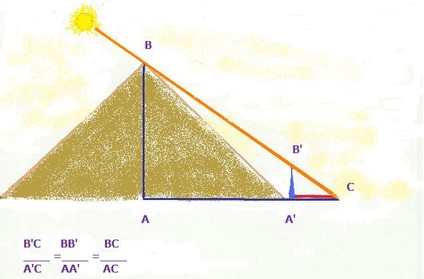
Nel mondo greco è Talete (624 -548 a.C. circa), ci racconta Erodoto, che affronta l’argomento predicendo l’eclisse totale di Sole verificatasi il 28 maggio 585 a.c. Talete avvalendosi di una semplice asta conficcata verticalmente nel terreno, ci dà la soluzione per conoscere l’altezza di oggetti grandi e lontani (ad es. una piramide) misurando la lunghezza della loro ombra. Il caso più facile è quando il Sole è alto 45°, la lunghezza dell’ombra dell’asta è uguale alla sua altezza e così vale per la piramide in proporzione alle diverse altezze del Sole. Questa è un’applicazione del teorema attribuito a Talete che forse egli formulò proprio osservando i raggi solari paralleli e le loro ombre che generano triangoli simili. Con il teorema di Pitagora, che nacque circa cinquant’anni dopo Talete, il problema si sarebbe potuto risolvere senza l’ausilio dell’ombra.
Aristotele (384 -322 a.C.) afferma che la Terra è sferica perché durante l’eclissi lunare la linea che delimita la sua ombra è curva.
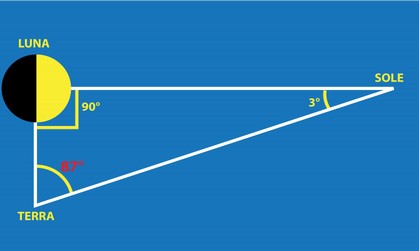
Aristarco (310 -230 a.C.) fu il primo aperto sostenitore del moto terrestre attorno al Sole. Misurando l’angolo tra Luna e Sole con vertice sulla Terra quando la Luna è in quadratura (al primo e all’ultimo quarto l’angolo tra Terra e Sole TLS è retto) spiegò come trovare il rapporto tra le distanze TS e TL. Purtroppo munito probabilmente di una semplice diottra (asta di puntamento su scala graduata) non riuscì a misurare con la precisione necessaria l’angolo LTS che valutò in 87° e credette che la distanza del Sole dalla Terra fosse 18/20 volte maggiore di quella della Luna dalla Terra. In realtà l’angolo è 89° 51’ e quindi il rapporto è di circa 390 volte. Solo nel XVII secolo , dopo accurate osservazioni, si riuscì a determinare che la Terra dista mediamente dalla Luna 384.400 Km e dal Sole 149.600.000 Km.
DIOTTRA
Guardando il cono d’ombra durante l’eclissi totale di Sole egli costatò che i diametri apparenti di Luna e Sole sono uguali (circa 31’) e sottendono lo stesso angolo, quindi, conoscendo la distanza TS e TL, si possono calcolare i loro raggi reali e le rispettive grandezze. In pratica il diametro del Sole sarebbe per Aristarco 18/20 volte quello della Luna. La teoria formulata è giusta, ma il calcolo è viziato dalle misure degli angoli. Il diametro equatoriale del Sole 1.391.000 Km è 400 volte quello della Luna che misura 3476 Km. Aristarco ancora una volta individua la soluzione corretta del problema. Quel che conta per lui è il metodo e non il risultato che è solo una conseguenza, ma non conviene qui addentrarci in speculazioni filosofiche che ci porterebbero a fare paragoni con la nostra attuale civiltà, che sotto certi aspetti va nella direzione opposta.
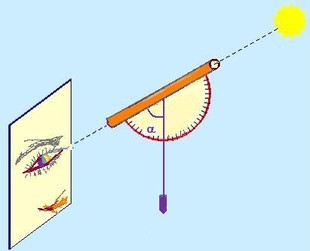
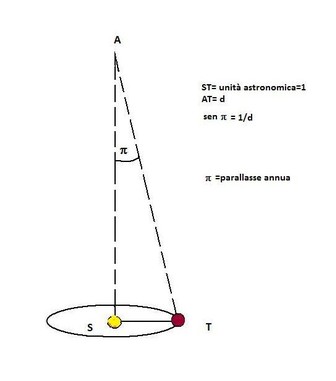
Osservando le stelle e sulla base dell’ipotesi che esse siano fisse, individuò l’angolo parallattico. Esso ad esempio può essere generato dal moto di rivoluzione della Terra sulla sua orbita che sposta il punto di vista dell’osservatore. Osservando il moto apparente delle stelle fisse si può calcolarne la distanza dalla Terra. Un triangolo rettangolo dove il Sole è vertice dell’angolo retto formato dal semiasse maggiore dell’orbita terrestre normale alla congiungente Stella- Sole. La Stella è vertice dell’angolo di parallasse da cui si vedrebbe il semiasse. Misurare l’angolo parallattico di una stella è molto difficile (inferiore a un secondo di grado) e solo dai primi decenni dell’ottocento gli astronomi furono in grado di fare calcoli precisi sulle distanze stellari.
Marco Vitruvio Pollione (I sec. a.C.) nel suo famoso trattato De Architectura fa un elenco degli orologi solari conosciuti e attribuisce ad Aristarco il " discum in planitia" e l’"hemispherium" quest’ultimo forse erroneamente. Il primo disegnato su di una superficie piana si pensa possa derivare per proiezione (ideata da Aristarco) dal secondo che rappresentava mezza sfera celeste Inclinata secondo la latitudine del luogo, scavata e disegnata con meridiani e paralleli in un blocco di pietra al cui centro era posto uno stilo verticale. Questo tipo di orologi, che nel tempo subirono una certa evoluzione, rientra nella categoria generale degli "Scaphen ". L’"hemicyclium" appunto che Vitruvio attribuisce a Beroso il caldeo (III sec.a.c.) fu un’ evoluzione dell’hemispherium (probabilmente anche questo ideato da Beroso), in esso non compaiono più le linee al di sotto del tropico del cancro che sono inutili e lo stilo è posto orizzontalmente.
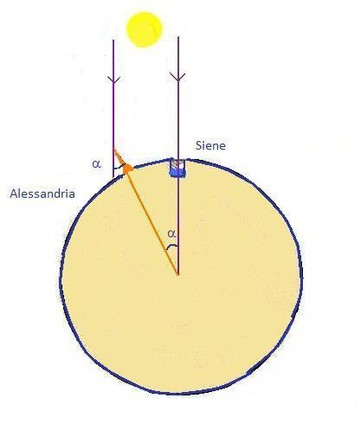
Della sfericità della Terra è convinto Eratostene (275 -195 a.C.) erudito in astronomia, geografia, matematica e direttore della biblioteca di Alessandria. Con la misura dell’ombra di uno stilo verticale installato ad Alessandria a mezzogiorno del solstizio estivo, trova l’altezza del Sole. Sapendo che Siene (Assuan) è molto vicina al tropico del Cancro, dove il Sole è allo zenit e quindi non fa ombra, determina l’angolo al centro della Terra 7° 12’, che è 1/50 dell’angolo giro, cui corrisponde l’arco di circonferenza terrestre che copre la distanza tra Siene e Alessandria che sono circa sullo stesso meridiano. Calcolando cinquanta volte la distanza tra Alessandria e Siene circa 250.000 stadi (pressappoco 790 km) Eratostene ottenne la misura di 39.400 Km che è molto prossima a quella reale media di 40.000. Cleomede racconta che Eratostene per questa misurazione si fosse avvalso in Alessandria di un hemispherium.
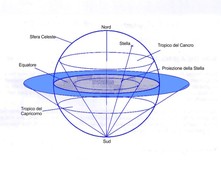
Eratostene è ritenuto l’inventore della sfera armillare (detta anche astrolabio sferico) . Una sorta di mappamondo composto di un certo numero di cerchi (in latino armillae = anelli) come quelli dell’equatore celeste, dell’eclittica, del meridiano attraversati dall’asse del mondo.
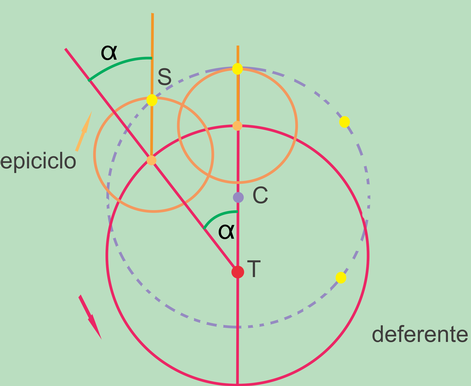
Apollonio di Perga (262 -190 a.C.) ideò gli epicicli per spiegare le anomalie del moto solare che risultano dalla differenza di durata delle stagioni. Pitagora (571-497 a.C.circa) riteneva che l’Universo fosse basato sul numero e quindi fosse un tutto ordinato (kosmos). Platone (428-348 a.C.circa) come già Pitagora concepisce il globo celeste mobile dove al suo centro sta la Terra immobile. Il Sole orbita a velocità costante intorno alla Terra percorrendo un cerchio perfetto. Apollonio per uniformarsi alla concezione Platonica immaginò la Terra al centro di un’orbita detta deferente sulla quale si sposta in senso antiorario il centro dell’orbita solare (epiciclo) con il Sole che ruota in senso orario. La combinazione di questi moti durante l’anno descrive un’orbita con lo stesso diametro di quella deferente, ma decentrata rispetto a essa. Tramite quest’orbita artificiosa Apollonio spiega le anomalie solari e dei pianeti facendo tornare pressappoco i conti. Dall’epoca di Platone in avanti la matematica e l’astronomia cominciano a guadagnare autonomia rispetto alla filosofia che fino allora era considerata l’unica forma di scienza. Diversamente dalla cultura orientale che mira a realizzare l’armonia con "l’altro da sé" attraverso l’accettazione del divenire e dell’indefinito, la civiltà occidentale ama affermare le idee, "il sé" attraverso la ragione. Abbiamo svariati esempi nella storia che quando all’uomo occidentale non è stato possibile affermarsi con la ragione ha imposto le proprie convinzioni con la forza. Sovente Il pensiero filosofico ha anticipato e ancora precede quello scientifico che tendenzialmente mira a soddisfarlo e quando vi riesce in buona fede, è un successo per entrambi. Se Apollonio trovò il modo di armonizzarsi con i preconcetti della scienza del suo tempo a cui aveva creduto , così non fu ad esempio per Giordano Bruno, Tommaso Campanella e Galilei rispetto ai dogmi scientifici della Chiesa ai quali si opposero, ma alla fine dovettero soccombere .
Vitruvio attribuisce ad Apollonio l'ideazione dell'orologio solare denominato "pharetram" di cui però non si conosce la forma.
Apollonio è conosciuto soprattutto per la sua opera principale sulle sezioni coniche . La teoria delle coniche trova applicazione anche in gnomonica. Il Sole con il suo moto annuale cambiando declinazione descrive dei coni le cui sezioni spesso si vedono tracciate sugli orologi solari. Esse sono differenti in funzione dell’inclinazione del quadro rispetto al piano equatoriale.
Ipparco (190 a.c.-120 a.C.) è da molti ritenuto il padre della scienza astronomica. A lui si deve, tra l'altro, la scoperta della precessione degli equinozi di cui parliamo a parte in un capitolo dedicato. Sulla base delle conoscenze dei Caldei e Babilonesi e di Apollonio perfezionò gli epicicli. Con Ipparco la scienza astronomica passa da descrittiva a predittiva grazie anche all’adozione del sistema sessagesimale dei babilonesi utile per la costruzione delle tavole astronomiche. Da alcuni gli è stata attribuita l’invenzione dell’astrolabio che è un calcolatore portatile analogico. La sfera celeste è rappresentata come se fosse schiacciata sul piano dell’equatore. Sullo stesso piano e concentrici all’equatore sono tracciati il cerchio del tropico del capricorno all’esterno e il tropico del cancro all’interno. L’eclittica con le costellazioni e le stelle più note decentrata e mobile interseca l’equatore ruotando sul disco detto rete. Un regolo imperniato al centro dello strumento sopra i dischi, serve a fare svariati calcoli riguardanti le stelle come ad esempio: ascensione retta, declinazione, altezza. Sul retro è fissata un’alidada che serve soprattutto a misurare altezze e azimut, ma anche per rapportare i giorni dell’anno con la posizione del Sole nello zodiaco. Sulla parte bassa del retro un rettangolo indica alla base l’umbra recta e con l’altezza l’umbra versa. Usando l’alidada si possono misurare altezze, distanze, azimut in topografia senza dover fare ricorso a calcoli complessi. Sulla stessa faccia sono tracciate le ore ineguali che si possono convertire in ore uguali riportando le misure sul fronte nello strumento. L’astrolabio si basa sulla proiezione stereografica e si attribuisce la sua invenzione a Ipparco proprio perché egli studiò a fondo questo tipo di proiezione e probabilmente ebbe l’idea di mettere il punto di vista al polo sud.
RECTO VERSO
Ipparco non conosceva la geometria sferica e l’astrolabio gli avrebbe permesso di risolvere diversi problemi come ad esempio quello difficile di determinare il sorgere e il tramontare del Sole in base alla latitudine. Sappiamo che Teone di Alessandria (IV sec.) scrisse un trattato sull’astrolabio andato perso. Non si sa chi per primo abbia realizzato l’astrolabio. Giovanni Filipono (530) descrive le parti di un astrolabio. E’ noto che questo strumento, utile anche per la determinazione delle ore della preghiera, fu studiato e sviluppato dagli arabi dall’Ottavo Secolo. Dalla Spagna mussulmana il suo uso si diffuse in Europa, dove ebbe il periodo di suo massimo fulgore tra il XIII e XVII. Geoffrey Chaucer nel 1391 scrisse il Trattato sull’astrolabio contenuto all’interno del prologo dei Canterbury Tales. Ha importanza scientifica più che letteraria perché ,oltre a descrivere in modo semplice lo strumento, c’informa sullo stato della cosmologia del XIII secolo. Fu scritto in inglese per il figlio Lewis che non conosceva il latino, lingua dei dotti. L’astrolabio era usato da astronomi, ingegneri e navigatori. Quello nautico aveva una struttura più robusta e semplice per misurare l’altezza delle stelle, era forato per non subire i colpi di vento, fu utilizzato da Colombo, Magellano e altri navigatori. Col tempo si trasformò in ottante e infine in sestante. Nel Seicento, con l’avvento del telescopio e lo sviluppo della trigonometria, l’astrolabio perse importanza.
Abbiamo detto che Vitruvio elencò tutti gli orologi solari noti al suo tempo e nel suo trattato parla della necessità di conoscere l’analemma per costruire orologi solari. Il significato tradotto dal greco è "appoggio" che non vuol dire molto se non lo s’intende come un qualcosa di cui servirsi, a cui appoggiarsi per fare qualcos’altro. Vitruvio operava al tempo di Giulio Cesare e Augusto e intorno al 30 a.C. scrive il trattato De Architectura in X libri. Nel IX parla di astronomia,astrologia ,orologi solari e ad acqua. Egli dedica poche righe all’analemma che in sintesi definisce come una costruzione geometrica che si deduce dal cammino del Sole utile per la costruzione degli orologi solari. Spiega come costruirlo senza però fornire istruzioni di come usarlo. Dice solo che per capire il funzionamento degli orologi solari descritti nel suo libro è necessario conoscere l’analemma. Il metodo dell’analemma risale a Greci ed Alessandrini ed era nato per l’esigenza di semplificare i calcoli di matematici ed astronomici riconducendo problemi tridimensionali al piano. Su questo metodo di geometria descrittiva si è basata la tecnica della costruzione geometrica degli orologi solari nelle varie epoche, diciamo anche fino ai giorni nostri. Tolomeo un secolo dopo approfondirà anche questo argomento.
L’analemma consiste in una proiezione ortografica della sfera celeste sul meridiano locale. Con esso si possono misurare l’altezza del Sole,il suo azimut rispetto ad un’ora temporaria qualunque e la durata di quest’ultima, quindi anche l’ora del sorgere e del tramonto del Sole. Il trattato De Architectura fu scoperto solo nel ‘400. Si continuò ad usare l’analemma anche nei secoli successivi per la costruzione di orologi d’altezza,ma anche verticali, a ore francesi e italiche,azimutali analemmatici.
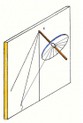
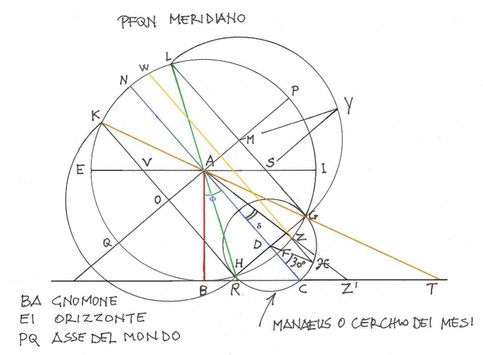
Il rapporto tra lo gnomone BA e l’umbra recta (cotangente) BC da l’apertura dell’angolo BAC sul piano meridiano all’equinozio che corrisponde alla latitudine j. BAC è uguale a IAP essendo PQ l’asse del Mondo. Il semicerchio LYG è la proiezione del parallelo di declinazione al solstizio estivo che il Sole percorre sulla sfera celeste . L’arco LY è l’arco diurno del Sole in quel giorno. LR è il raggio di luce all’omonimo solstizio e BR la relativa umbra recta. KT è il raggio del solstizio invernale. Il Manaeus o cerchio dei mesi permette di trovare la declinazione solare di un certo giorno di cui si conosca la longitudine celeste l. Questa si ottiene contando 1° al giorno dall’equinozio primaverile, per la precisione 360° divisi in 365,25 giorni sono 0°,985 al giorno. Più avanti parleremo dell’eclittica, dello zodiaco e della durata dell’anno che sono correlati . L’angolo C D icorrisponde a 30° dal punto g cioè all’inizio del segno dei Pesci che precede l’Ariete. ZW è il relativo parallelo di declinazione. L’analemma si potrebbe definire come il passepartout della gnomonica e per comprenderne bene l’uso bisogna conoscere la sfera celeste.(vedi capitolo dedicato )