ORIENTAMENTO DEL QUADRANTE - Le Meridiane di Alberto Rebora

CONSIDERAZIONI SULLA DECLINAZIONE DELLA PARETE

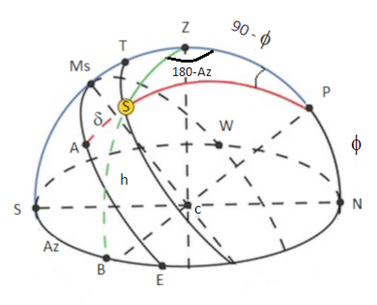
Per calcolare la declinazione della parete su cui s’intende realizzare un quadrante solare dobbiamo misurare l’azimut del  Sole. In astronomia è detto azimut a l’arco di orizzonte compreso tra il punto cardinale nord e il verticale passante per l’astro contato da 0° a 360° in senso orario (vedi sotto l’arco NB= a).Nei calcoli nautici si preferisce usare l’angolo azimutale Z (sempre ≤180)contato da nord (o sud in base al nome della latitudine) verso est o ovest.(vedi sotto Z che qui coincide con l’azimut a ) In gnomonica  si usa l’angolo azimutale Az (supplementare di Z) misurato da sud (o viceversa da nord nell’emisfero australe) verso est o ovest da 0° a 180° con lo stesso segno dell’angolo al polo: positivo o negativo se l’astro si trova rispettivamente ad ovest o ad est del meridiano locale.    (vedi anche:Sfera Celeste)                                                 
                     

Z=180-Az
Nell’istante in cui l’ombra dello stilo ortogonale HS (vedi immagine seguente) si sovrappone alla linea verticale HM (tracciata a piombo sul muro dal suo piede) il Sole si trova sul piano perpendicolare alla parete, quindi il suo  angolo azimutale Az coincide con la declinazione della parete. Se questo avviene a mezzogiorno vero locale, sappiamo che in quell’istante il Sole si trova a sud, Az è nullo e così anche la declinazione della parete che risulta orientata secondo la direzione EW.

Rilevamento all’istante del  passaggio del Sole al meridiano locale (Az = 0°)   

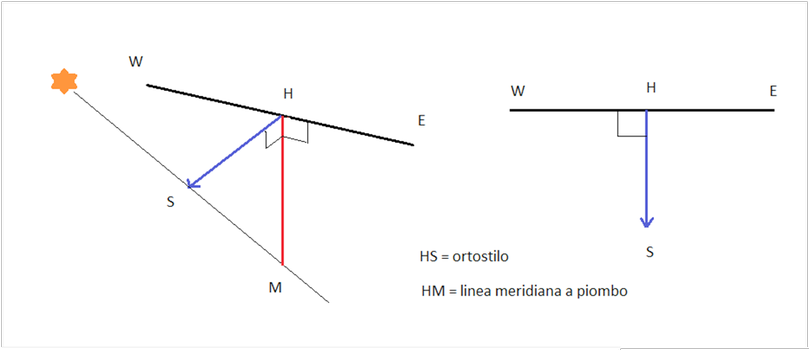
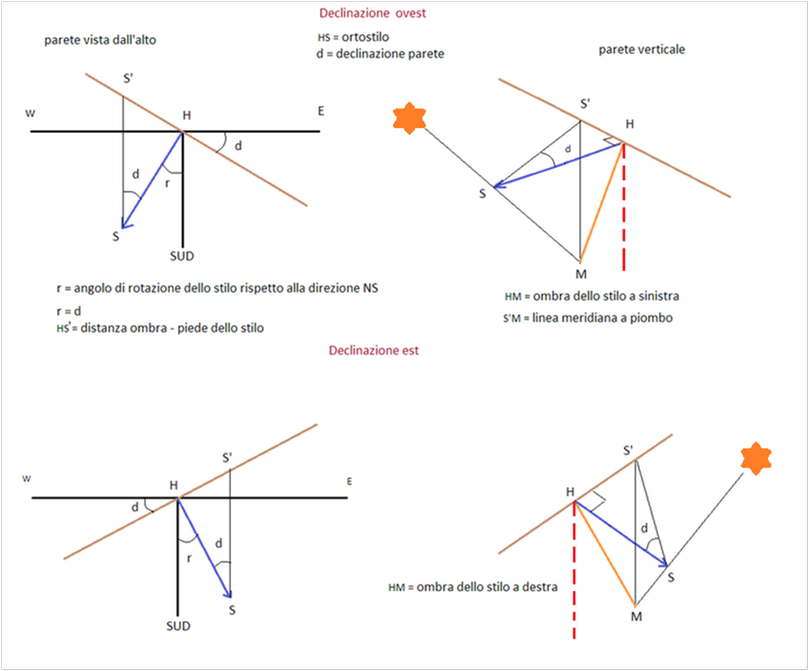
Se a mezzogiorno vero l’ombra dell’ortostilo non coincide con la verticale, possiamo calcolare la declinazione del quadrante misurando sul muro lo spostamento dell’ombra rispetto al piede dell’ortostilo. Se l’ombra, dal punto di vista dell’osservatore, si trova a sinistra dello stilo (o del filo a piombo che si usa con la tavoletta) la declinazione è ovest , se cade a destra la declinazione è est.

Dal punto di vista azimutale l’angolo di rotazione r dello stilo rispetto a sud corrisponde alla declinazione d.

tangd=HS'/HS                       

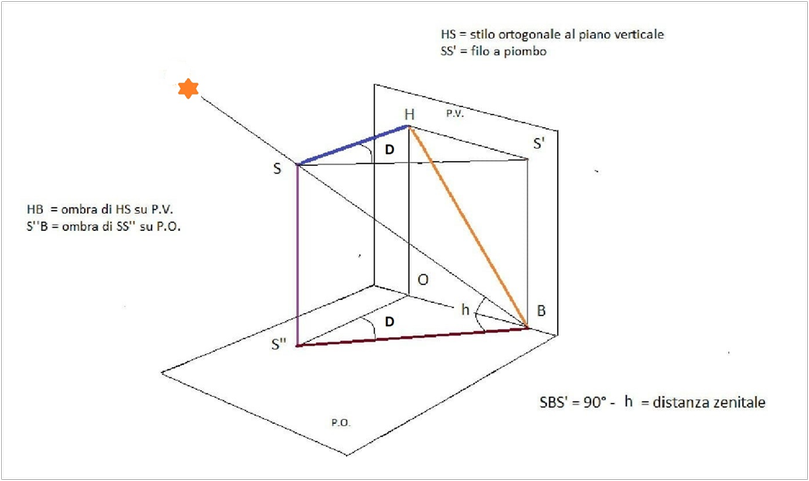
Rilevamento  in istanti qualsiasi ( Az ≠ 0°)
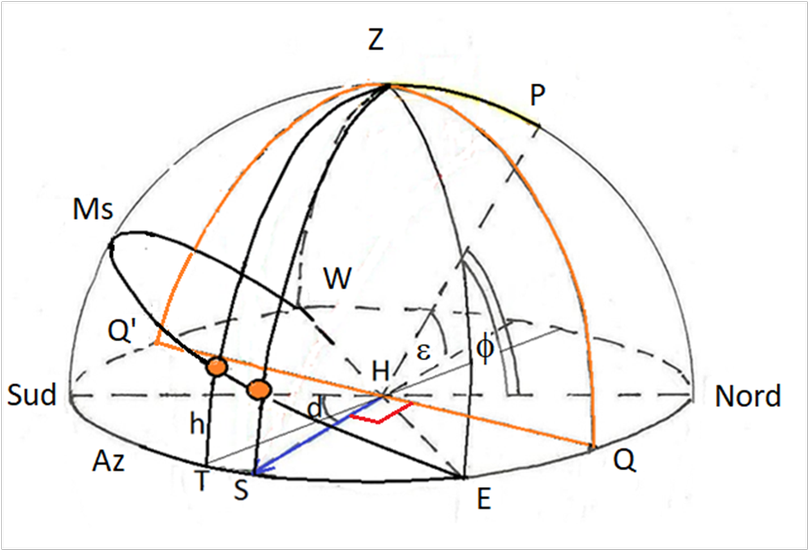
Come si vede dall’immagine seguente con un quadrante declinante , quando Az è misurato in S i raggi solari sono ortogonali al quadro Q’ZQ, l’ombra è verticale (si legge l’ora sustilare) e la declinazione è d = Az (vedi più avanti fig.2). Se si considera Az quando il Sole si trova al meridiano che passa per T con altezza h, per ottenere d dobbiamo immaginare di dover riportare l’astro in S compensando Az con l’angolo di spostamento dell’ombra che rileveremo sul muro.

Possiamo trovare la declinazione del quadrante a un’ora diversa dal passaggio del Sole al meridiano superiore, se calcoliamo l’azimut del Sole al momento della misurazione e lo sommiamo algebricamente all’angolo di spostamento tra lo stilo (o il filo a piombo) e la sua ombra. L’azimut prenderà,come s’è detto in precedenza, segno negativo quando il Sole si trova a est del mezzogiorno solare e positivo in posizione pomeridiana. L’angolo di spostamento che chiamiamo D sarà negativo con ombra a destra e positivo con ombra a sinistra dello stilo. Di conseguenza la declinazione prenderà segno negativo se a est e positivo a ovest.


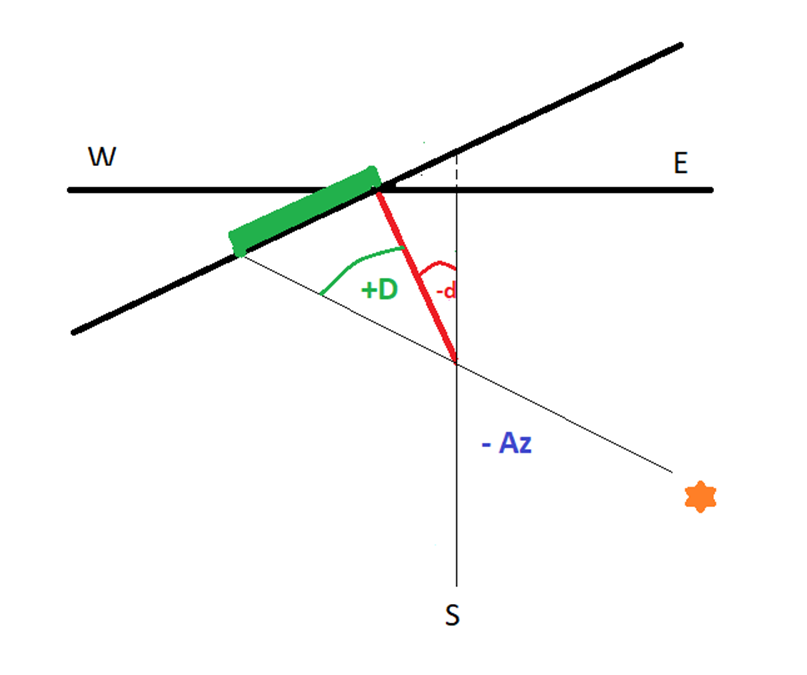
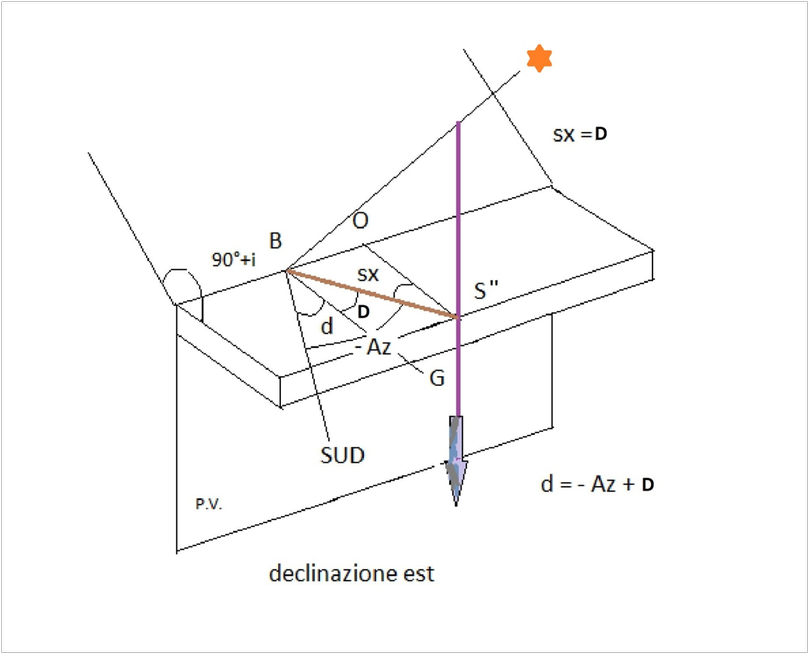
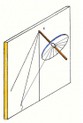
La prima immagine che segue mostra l’ipotesi in cui il Sole si trovi a est prima che i suoi raggi siano normali alla parete. L’angolo azimutale ,qui negativo, è più ampio dell’angolo di spostamento e quindi il risultato con segno meno stabilisce che la declinazione del quadrante è a est.

fig.1                                                    

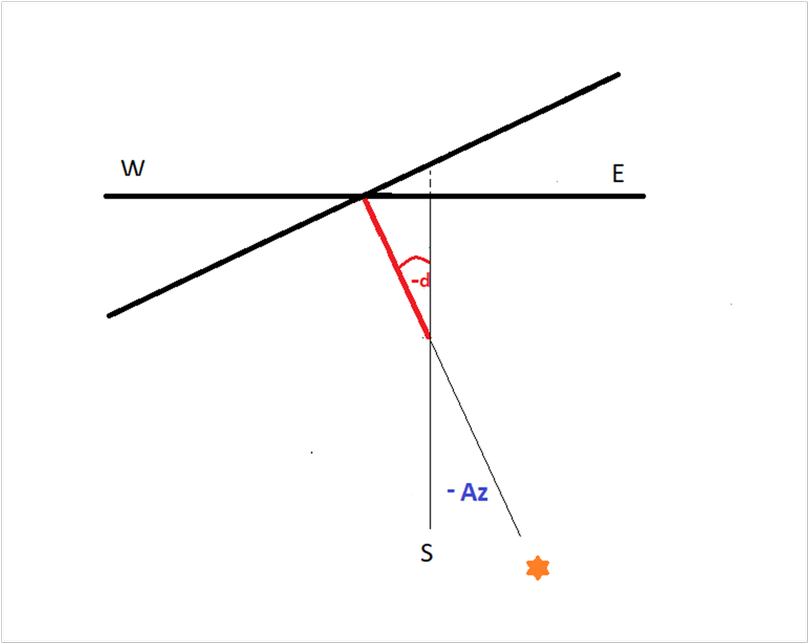
L’immagine successiva mostra il Sole a perpendicolo su di una parete declinante est dove l’azimut negativo coincide con la declinazione. In quel momento l’ombra sul quadrante è verticale e segna l’ora sustilare che è anche l’asse di simmetria dell’orologio.

fig.2   
                
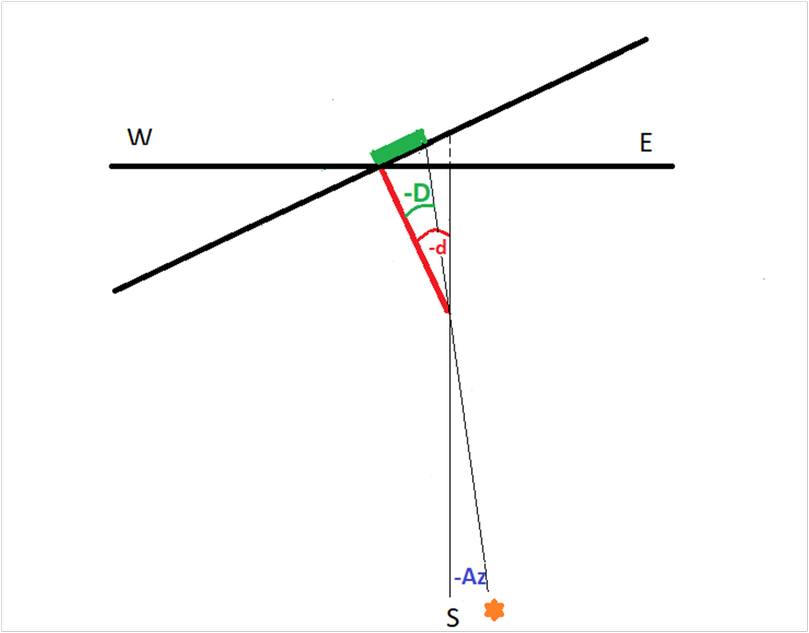
Il disegno seguente mostra quando il Sole si trova ancora a est, ma ha superato il piano normale al quadrante. L’ombra dello stilo a destra esprime un angolo di spostamento negativo che sommato all’angolo azimutale negativo danno il valore della declinazione negativa quindi a est.

fig.3

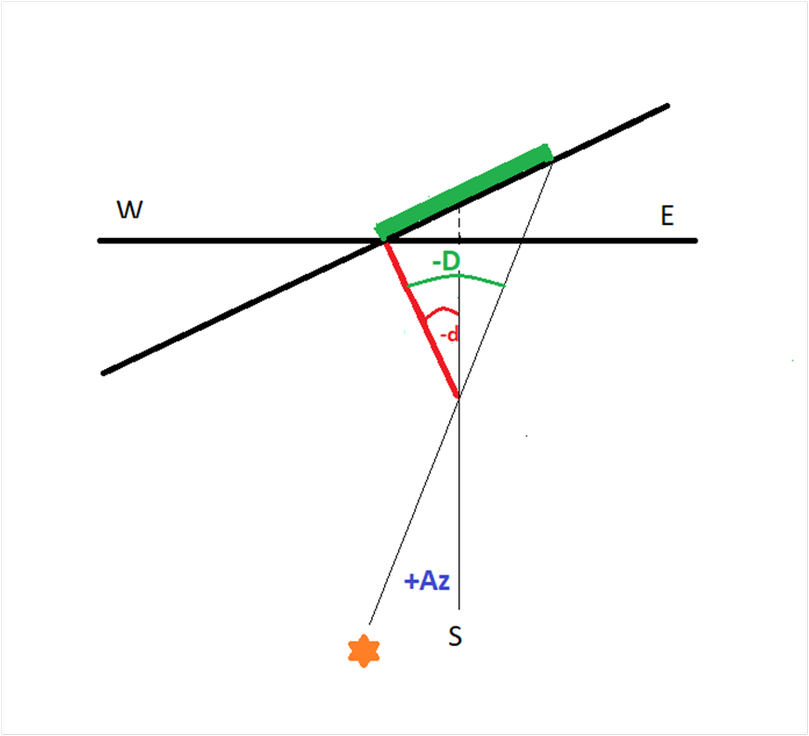
Segue il caso in cui  Az  è positivo avendo superato la linea di mezzogiorno. La declinazione risulterà ancora est poiché lo spostamento D negativo sarà sempre maggiore di Az misurato dopo mezzogiorno. E’ opportuno che le misurazioni dell’ombra dello stilo non avvengano né in momenti troppo vicini all’ora sustilare ne troppo lontani. In particolare se la declinazione è est converrà non spingersi troppo nelle ore pomeridiane dove le ombre sono molto lunghe e spesso non risulta facile fare misurazioni di precisione.

fig.4

La casistica per quanto riguarda la declinazione ovest è simmetricamente la stessa, quindi è superfluo esporla.
Come detto all’inizio  Az prende il segno dell’angolo al polo negativo a est, positivo a ovest. L’azimut può essere ottenuto utilizzando le Tavole ABC per il calcolo dell’azimut  o meglio ancora con una semplice lettura consultando le Tavole a soluzione diretta per il calcolo delle rette d’altezza (l. l. 3137)edite dall’Istituto Idrografico della Marina - Genova.  

Altrimenti dalle note formule di trigonometria sferica che legano l’angolo al polo con l’altezza e la declinazione dell’astro con il suo azimut (vedi qui la pagina de: la Sfera Celeste) e tenuto conto che cos180°-Az=- cosAz  si ricava :   

cosAz=(senφsenh-senδ)/cosφcosh (1) (formula di Eulero)

Con latitudine φ > 0 la regola è:  

d = Az + D   somma algebrica  dove D è negativo con ombra a destra e positivo con  ombra a sinistra
Per trovare l’angolo di spostamento D  è sufficiente misurare sulla parete la distanza HS’ tra il piede dello stilo ortogonale e la verticale passante per l’estremità dell’ombra, oppure sul piano orizzontale la corrispondente distanza OB dell’estremità dell’ombra del filo a piombo e la retta ortogonale dal filo al muro.

fig.5
Così conoscendo la lunghezza dello stilo HS, che equivale alla distanza del filo a piombo dal piano verticale, possiamo trovare lo spostamento D misurando, ad un istante noto, l’ascissa HS’= OB con la seguente formula:

tangD= HS'/HS

Oppure misurando l’ordinata S’B =OH

cosD = HS/S'B tangh *

Se non si conosce con precisione la lunghezza dello stilo se ne può fare a meno combinando le due formule precedenti e misurando le coordinate dell’estremità OB=HS’  e OH=S’B della sua ombra.

                                                                                              senD=(HS'/S'B)tangh                                                                                                                                                 
L’altezza del Sole h si può ricavare dalla solita

               senh = senφsend + cosφcosδcosP (2)

Ne consegue che non è necessario conoscere l’istante della misurazione per calcolare l’altezza del Sole se sono conosciuti lo spostamento D e la lunghezza dello stilo che possiamo ottenere con la seguente formula:                                                                                     
                                                                                           tangh = (S'B/HS) cosD (3)
che deriva dalla *

Il filo a piombo si usa con la tavoletta appoggiata alla parete tenuta in bolla nelle due direzioni perpendicolari tra loro. Con essa si può misurare anche la declinazione del quadrante inclinato.

La direzione dell’ombra destra o sinistra  qui non è indicativa dell’orientamento della declinazione che è ovest con d > 0 e est con d < 0. In alternativa al filo, che è difficile da tenere fermo,  si può usare un parallelepipedo che misuri, ad esempio 20x5x5 cm(misure da adattare alle proprie esigenze) da orientare in modo che non faccia ombra lateralmente. Si evitano così anche le penombre.  
Esempio di calcolo della declinazione gnomonica  dopo la rilevazione dell’ombra solare con tavoletta e filo a piombo
Dati:
j  Lat.44°46’37"N      l Lon.8°41’42"E.
Giorno 24/5/14.
TMF alle ore 13 55’ 25" di tempo medio del fuso dedotta l’ora legale.  

Eqt   equazione del tempo – 3’  11"   C. L. costante locale  25’ 13".
O.V. Ora vera (TMF – EqT - C.L.)  ore 13 33’ 23" = ore 1.5564 dopo il mezzogiorno.
P angolo al polo  1,5564 x 15° = + 23°,3461.
d Declinazione solare = +20°,808.         
HS= 13,2 ;  HS’ =8 ;    arcotang (8/13,2) =31°,22  angolo di spostamento D con segno + se l’ombra è a sinistra.                                                                                                                                                            
Da cui con la 2) si ricava l’altezza solare  h = 59°,254.
Altrimenti  l’altezza solare può essere calcolata,  con la formula (3) senza conoscere il tempo d’osservazione, purchè  si conosca (vedi fig. 5) l’ordinata OH=S’B 25,94, l’angolo D  e la lunghezza dello stilo.
Quindi con la 1)  si calcola AZ azimut del Sole rispetto a sud = +46°,43  positivo come P.
d = AZ + D = 46°,43 + 31°,22 = 77°,65 ovest
Conviene sempre fare  più misurazioni che si ripeteranno nei giorni successivi se si opera a mezzogiorno vero, oppure in tempi diversi con almeno tre rilevamenti  distanziati tra loro di  5’ intercalando l’uso della tavoletta con quello dell’ortostilo.La tolleranza  tra i vari risultati non dovrebbe superare il decimo di grado.  Il metodo di rilevamento combinato descritto  è sufficientemente affidabile per i comuni orologi da muro. Un altro metodo per calcolare la declinazione del muro è  quello di traguardare il momento del passaggio del Sole sulla parete  al mattino o al pomeriggio e rapportarlo a quello del passaggio al meridiano. In generale è bene evitare di fare misurazioni quando il Sole è basso sull’orizzonte per ridurre al minimo  l’effetto d’incremento dei valori d’altezza del Sole causato dalla rifrazione atmosferica. Comunque nelle ore piene della giornata dalle 9.30 alle 15.30  la rifrazione è praticamente ininfluente.
Ovviamente in casi particolari  l’utilizzo di un teodolite oppure di uno strumento laser permettono misurazioni molto più precise, si veda ad esempio quando il Sole sia pressoché  parallelo alla parete  e/o il quadro risulti scarsamente  declinante oppure si vogliano realizzare opere di grandi dimensioni.